
My colleague Denise and I have been working in Grade 3 classrooms in two of our schools for the past few weeks, engaging students in problem solving using concrete materials. Our focus has been on concepts where our board has generally struggled , based on EQAO data over time. What's really interesting to us is that the data we used has led us to uncover a common thread. We realized that students are often asked to build and compare when problem solving. At the same time, we notice that many students don't build, which means they can't compare. Hmmm...I think we are on to something, here. We decided to use this common thread to help students to build a stronger understanding of equality. These photos document some of the learning we observed during lessons around equations and equal amounts of money.
| | In the first lesson, we decided to tackle the concept of equations in a very visual way. Our students have been exposed to cube lines this year, as a way to introduce the number line, and help them to see relationships between numbers. We decided to leverage this model to think about equations. |
What amazed us was the simplicity of the game that we used to help students to build their own equations. Each of us started with a stick of 30 cubes in two colours, with 5 cubes per colour in a repeating pattern (as described by the students). The students readily described our two lines as equal, and we were able to prove this by placing one line on top of the other. This creates a pretty cool visual. The cube lines became the equals sign. This led students to use the cube lines to solve for missing values in equations, by describing the actions they took to make their two cube lines equal lengths.
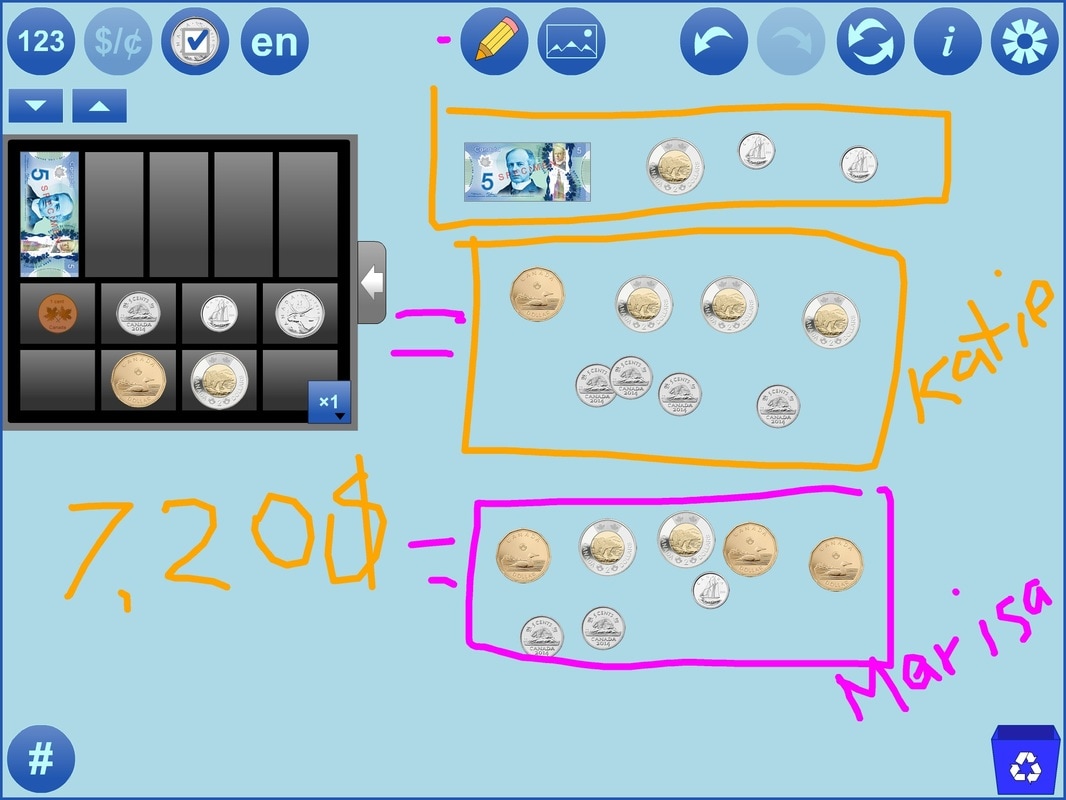
In the next lesson, we explored equal money amounts. At the beginning of this lesson, students made connections between the cubes lesson and equal amounts, which made it much easier to launch the idea of equal amounts of money. Pairs of students were given a paper bag with an amount of money between $5 and $7, which they needed to represent using different combinations of coins and bills. Using the mathies money app on a screen, we were able to model the different ways to represent equal amounts of money, in order to consolidate our understanding of the problem as a large group (see the image above for an example).
The power of connections across different models, strands and problem types really stood out to us as a result of these two lessons. The idea of equality resonates everywhere in mathematics, and yet it's an idea that seems to stump many students. That leaves me wondering why? How might we make more explicit connections between big ideas (like equivalence) in order to help all students see the idea more clearly?
In the next lesson, we explored equal money amounts. At the beginning of this lesson, students made connections between the cubes lesson and equal amounts, which made it much easier to launch the idea of equal amounts of money. Pairs of students were given a paper bag with an amount of money between $5 and $7, which they needed to represent using different combinations of coins and bills. Using the mathies money app on a screen, we were able to model the different ways to represent equal amounts of money, in order to consolidate our understanding of the problem as a large group (see the image above for an example).
The power of connections across different models, strands and problem types really stood out to us as a result of these two lessons. The idea of equality resonates everywhere in mathematics, and yet it's an idea that seems to stump many students. That leaves me wondering why? How might we make more explicit connections between big ideas (like equivalence) in order to help all students see the idea more clearly?



 RSS Feed
RSS Feed
