In contrast, knitting was a procedural task for me. I found a pattern and followed it. I made fair isle sweaters, scarves, mitts, hats, and simpler things like dishcloths and afghan squares. I sourced a pattern, gathered materials and iterated the pattern to the best of my ability. I found myself doing a lot of counting and marking stitches. What I didn’t do is THINK about the pattern and how it worked. I didn’t take the time to understand what I was doing. I was just great at following instructions. I expressed my creativity with colour combinations at times, but mostly hoped my product would turn out like the picture.
Recently, my approach to knitting has completely changed. I’ve been knitting differently, with greater confidence, one might even say with reckless abandon. I’m giving my big sister a run for her money.
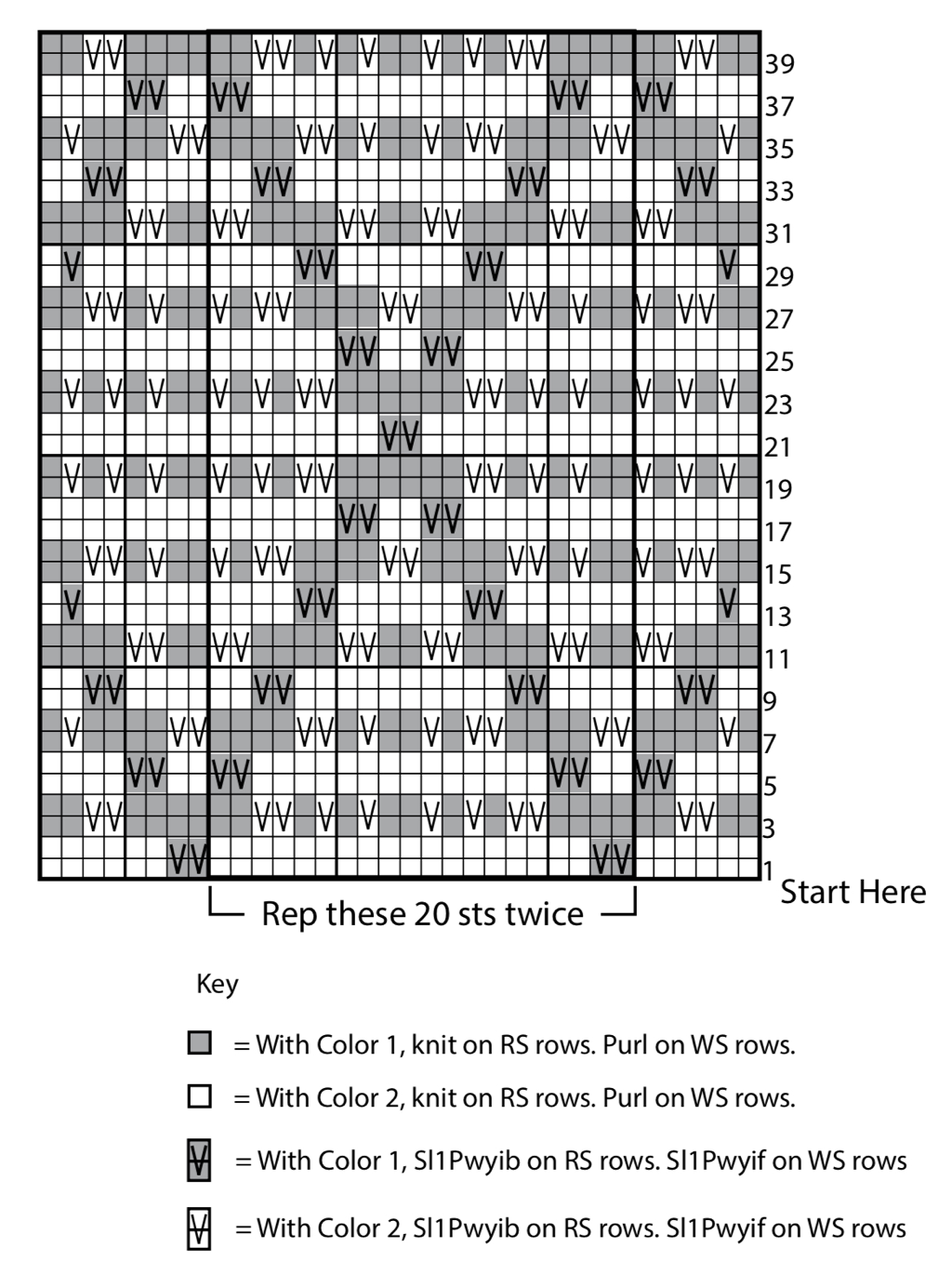
| Last November, my husband and I took a long road trip from Sudbury, Ontario to Florida and back. Knowing I would spend a lot of time in the passenger seat, I decided to knit cushion covers and mitts for my kids for Christmas. Armed with a couple of online free patterns, a bag of assorted yarns and needles, we hit he road. Initially, I applied my usual strategy of following a pattern to a T, but the product didn’t work out. I had brought wool that was too thick, so the stitch counts produced sizing which wasn’t going to work. I could have become frustrated and given up, but I was determined to solve the problem. I quickly realized I had to rely on myself. Google had not provided me with a quick solution. Instead, I needed to leverage my existing knowledge and make a connection. Considering the pattern I already had, I thought about it’s structure. The pattern was set up as grid, with some squares blocked with v, to mark a purl. Some squares were also shaded to represent a second colour. 💡 💡 💡 💡 💡 💡 💡 This was a lightbulb moment for me! I realized I could apply my understanding of patterning. The mathematics inherent in this problem surfaced for me. I noticed:
Since grids are rectangular structures, I determined I could adapt the grid to adjust the size and shape of my finished piece. Similarly, I could adapt the attributes (variables) to create different texture and colour patterns. This was a math problem I could solve. I did the math, determining the number of stitches required to create the correct finished width for my pillow cover. This led to a new problem: revising the grid to create a new pattern chart. | https://www.yarnspirations.com/ca-en/bernat-knit-diamond-mosaic-cushion-cover/BRK0520-010097M.html |
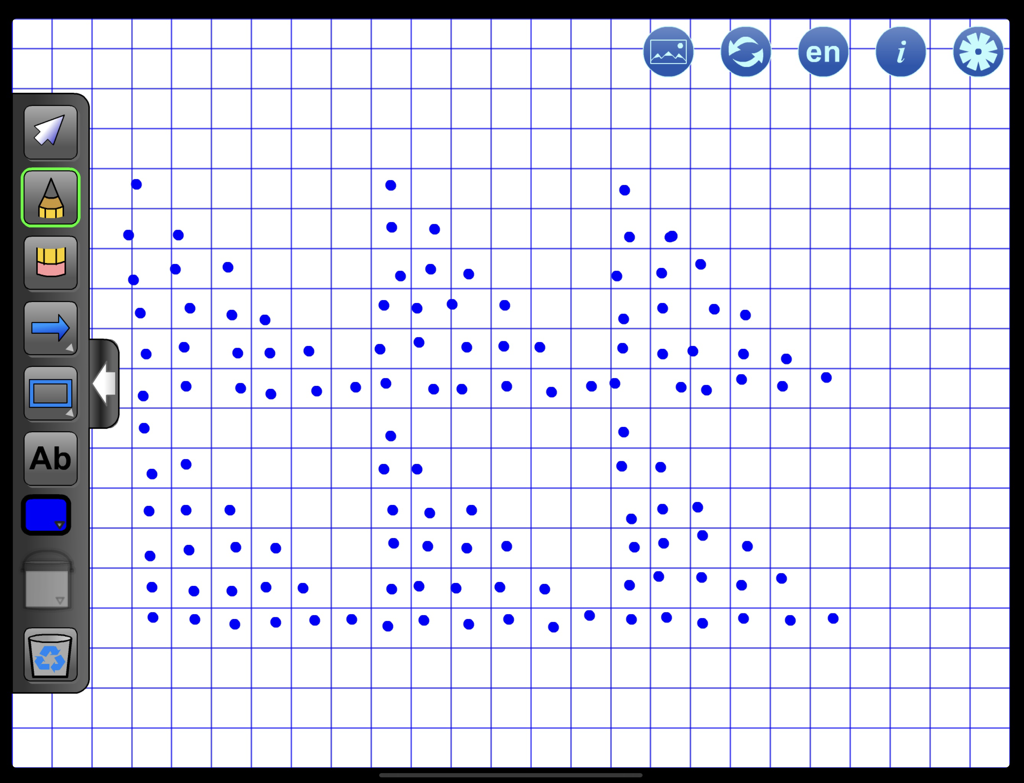
| Aha! Another math problem I could solve. With some tweaks to the stitch count, I thought about how to structure a pattern in groups of 6 stitches. Over several rows, 6 stitches allowed for a variety of design combinations. I used Mathies Notepad to test the pattern I had planned and give myself a familiar structure to follow. I was using what I knew and connecting two knowledge systems together. I had begun to think about knitting as patterning. |
I was making sense of the pattern’s underlying code. The pattern core became visible and I was thinking in chunks. With this realization, my confidence grew. The mathematical connections were suddenly crystal clear. The textures created when knitting were the result of the execution of a binary code, where each stitch was either a knit or purl. The connections between coding and patterning emerged.
This realization freed me to create unlimited patterns. With each subsequent pillow cover, I took more risks, creating increasingly complex patterns, running contrasting patterns in bands, even thinking about the relationships between widths of bands, using ratios that I knew would be pleasing to the eye. Wait, what? Ratios played a role too?
I no longer used a written pattern at all, relying instead on my ability to deal with the small blocks stitches as units. I noticed the math inherent in my work and creativity burst forth from there.







































 RSS Feed
RSS Feed
